Grados a Radianes.
Con esta simple fórmula podemos convertir Grados en Radianes.
Radianes a Grados.
Con esta simple fórmula podemos convertir Radianes en Grados.
Como Convertir los decimales a Minutos y Segundos.
Ejemplo.
45.891°
1ro tomamos los decimales .891 lo multiplicamos por 60 y nos da de resultado 53.46.
2do tomamos los nuevos decimales que obtuvimos .46 los multiplicamos por 60 y nos da como resultado 27.6 que se redondea a 28.
3ro Resultado final: 45° 53' y 28'' Osea 45 grados, 53 minutos y 28 segundos.
Fuente: http://www.ehowenespanol.com/conversion-grados-radianes-como_113664/
De Jesús Vargas Daniel.
CCH-Naucalpan.
201-A
Matemáticas II.
jueves, 2 de mayo de 2013
Ley del Seno y Coseno.
Ley del Seno:
Nos demuestra que los lados de un triángulo son proporcionales a los senos de los ángulos opuestos.
Ley del Coseno:
Nos demuestra que el cuadrado de un lado es igual a la suma de los cuadrados de los otros lados menos el doble del producto de estos lados por el coseno del ángulo comprendido.
a² = b² + c² - 2 bc * Cos (A)
b² = a² + c² - 2 ac * Cos (B)
c² = a² + b² - 2 ab * Cos (C)
Fuente: http://docente.ucol.mx/narahita/leyes/sen2.htm
De Jesús Vargas Daniel.
CCH-Naucalpan.
201-A
Matemáticas II.
Nos demuestra que los lados de un triángulo son proporcionales a los senos de los ángulos opuestos.
Ley del Coseno:
Nos demuestra que el cuadrado de un lado es igual a la suma de los cuadrados de los otros lados menos el doble del producto de estos lados por el coseno del ángulo comprendido.
a² = b² + c² - 2 bc * Cos (A)
b² = a² + c² - 2 ac * Cos (B)
c² = a² + b² - 2 ab * Cos (C)
Fuente: http://docente.ucol.mx/narahita/leyes/sen2.htm
De Jesús Vargas Daniel.
CCH-Naucalpan.
201-A
Matemáticas II.
Ecuaciones con Razones Trigonométricas.
Ejercicio 1.
Obtener el resultado de la siguiente función.
6 (SEN 30°) (COS 30°) + 8(TAN 30°) (COS 45°) =
Paso 1°: Obtener lo que esta dentro de paréntesis, osea lo senos y cosenos.
6 (0.5) (0.86) + 8 ( 0.57) (0.70) =
Paso 2°: Hacer las multiplicaciones correspondientes.
3 * 0.86 + 4.56 * 0.70 =
2.58 + 3.19 = 5.77
El resultado de esta función es 5.77.
De Jesús Vargas Daniel.
CCH-Naucalpan.
201-A
Matemáticas II.
Obtener el resultado de la siguiente función.
6 (SEN 30°) (COS 30°) + 8(TAN 30°) (COS 45°) =
Paso 1°: Obtener lo que esta dentro de paréntesis, osea lo senos y cosenos.
6 (0.5) (0.86) + 8 ( 0.57) (0.70) =
Paso 2°: Hacer las multiplicaciones correspondientes.
3 * 0.86 + 4.56 * 0.70 =
2.58 + 3.19 = 5.77
El resultado de esta función es 5.77.
De Jesús Vargas Daniel.
CCH-Naucalpan.
201-A
Matemáticas II.
miércoles, 1 de mayo de 2013
Funciones Trigonométricas II.
Problema 1.
Un teleférico recorre 8 metros y se eleva a una la altura de 1.5 metros ¿Cual sera el ángulo de elevación de la subida, y la distancia entre las 2 montañas entre las que se encuentra el teleférico?
Para saber el ángulo, usamos la función trigonométrica de Seno, ya que tenemos las medidas de cateto opuesto y la hipotenusa.
Nota: A = a ángulo.
Sen A = 1.5/8
Sen A = 0.18
A= Sen-¹ (0.18)
A= 10.36
Ya obtuvimos el ángulo ahora falta la distancia entre las montañas (x). Para obtener esto solo utilizamos teorema de pitagoras.
c² = a² + b²
8² = 1.5² + b²
64 = 2.25 + b²
64-2.25 = b²
61.75 = b²
7.85 = b
Y ya obtuvimos el lado restante del triángulo que es la distancia entre las 2 montañas.
De Jesús Vargas Daniel.
CCH-Naucalpan.
201-A
Matemáticas II.
Un teleférico recorre 8 metros y se eleva a una la altura de 1.5 metros ¿Cual sera el ángulo de elevación de la subida, y la distancia entre las 2 montañas entre las que se encuentra el teleférico?
Para saber el ángulo, usamos la función trigonométrica de Seno, ya que tenemos las medidas de cateto opuesto y la hipotenusa.
Nota: A = a ángulo.
Sen A = 1.5/8
Sen A = 0.18
A= Sen-¹ (0.18)
A= 10.36
Ya obtuvimos el ángulo ahora falta la distancia entre las montañas (x). Para obtener esto solo utilizamos teorema de pitagoras.
c² = a² + b²
8² = 1.5² + b²
64 = 2.25 + b²
64-2.25 = b²
61.75 = b²
7.85 = b
Y ya obtuvimos el lado restante del triángulo que es la distancia entre las 2 montañas.
De Jesús Vargas Daniel.
CCH-Naucalpan.
201-A
Matemáticas II.
lunes, 29 de abril de 2013
Funciones Trigonométricas.
Ejercicio 1.
Obtener las funciones trigonométricas y ángulos del siguiente triángulo.
Las funciones trigonométricas son 6 :
Seno, Coseno y Tangente. Seno se obtiene dividiendo Cateto opuesto/ Hipotenusa.
Coseno se obtiene dividiendo Cateto adyacente/ Hipotenusa.
Tangente se obtiene dividiendo Cateto opuesto / Cateto adyacente.
Y sus Inversas: Cosecante: Hipotenusa / Cateto Opuesto.
Secante: Hipotenusa / Cateto adyacente.
Cotangente: Cateto adyacente / Cateto opuesto.
(Los catetos se pueden identificar porque son los 2 lados con los que se forma el angulo de 90°)
Paso 1 : Obtener las funciones Trigonométricas.
Obtener las funciones trigonométricas y ángulos del siguiente triángulo.
Las funciones trigonométricas son 6 :
Seno, Coseno y Tangente. Seno se obtiene dividiendo Cateto opuesto/ Hipotenusa.
Coseno se obtiene dividiendo Cateto adyacente/ Hipotenusa.
Tangente se obtiene dividiendo Cateto opuesto / Cateto adyacente.
Y sus Inversas: Cosecante: Hipotenusa / Cateto Opuesto.
Secante: Hipotenusa / Cateto adyacente.
Cotangente: Cateto adyacente / Cateto opuesto.
(Los catetos se pueden identificar porque son los 2 lados con los que se forma el angulo de 90°)
Paso 1 : Obtener las funciones Trigonométricas.
Paso 2 : Obtener las Medidas de los Ángulos.
Para obtener la medida del ángulo que nos piden podemos despejar a seno así:
Nota A = angulo.
Sen A = 0.83
A= Sen-¹ (0.83)
A= 56.09°
Y esa es la medida del ángulo que nos piden.
De Jesús Vargas Daniel.
CCH-Naucalpan.
201-A
Maremáticas II.
Volumenes.
Ejercicio 1.
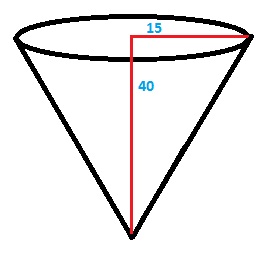
Calcula el volumen de un cono si el radio de su base mide 15 cm y la altura 40.
Solo debemos aplicar la formula para saber el volumen del cono : ¶ . r² . h / 3
Osea 'Pi' por radio al cuadrado por altura entre 3.
Paso 1: Solo sustituir en la formula y resolver loas operaciones.
¶ * 225 * 40 / 3
Resultado: 9424.77 cm ³
Y ese es el volumen del cono.
De Jesús Vargas Daniel.
CCH-Naucalpan.
201-A
Matemáticas II.
martes, 16 de abril de 2013
Areas.
Ejercicio 1.
Un espejo circular mide 1.25 metros de diámetro ¿Que área tiene?
Solo hay que saber que la formula para sacar el área de un circulo es 3.1416 x r^2. Osea pi por radio al cuadrado.
En este caso nos dan el diámetro, pero nosotros necesitamos el radio entonces dividimos el diámetro entre 2. Obtenemos .625.
Ahora ya aplicamos la formula, primero hacemos .625 al cuadrado, eso nos da de resultado .3906, y ya esto lo multiplicamos por pi, esto nos da de resultado 1.2271 y eso es el área del espejo.
De Jesús Vargas Daniel.
CCH-Naucalpan.
201-A
Matemáticas II.
Un espejo circular mide 1.25 metros de diámetro ¿Que área tiene?
Solo hay que saber que la formula para sacar el área de un circulo es 3.1416 x r^2. Osea pi por radio al cuadrado.
En este caso nos dan el diámetro, pero nosotros necesitamos el radio entonces dividimos el diámetro entre 2. Obtenemos .625.
Ahora ya aplicamos la formula, primero hacemos .625 al cuadrado, eso nos da de resultado .3906, y ya esto lo multiplicamos por pi, esto nos da de resultado 1.2271 y eso es el área del espejo.
De Jesús Vargas Daniel.
CCH-Naucalpan.
201-A
Matemáticas II.
lunes, 15 de abril de 2013
Áreas.
Ejercicio 1.
¿Cual es el perímetro de un terreno pentagonal si cada lado mide 13 metros?
Esto es muy fácil sabemos que un pentágono tiene 5 lados, y que cada lado mide 13 metros, entonces lo único que hay que hacer es multiplicar 5 x 13 = 65 m.
De Jesús Vargas Daniel.
CCH-Naucalpan.
201-A
Matemáticas II.
¿Cual es el perímetro de un terreno pentagonal si cada lado mide 13 metros?
Esto es muy fácil sabemos que un pentágono tiene 5 lados, y que cada lado mide 13 metros, entonces lo único que hay que hacer es multiplicar 5 x 13 = 65 m.
De Jesús Vargas Daniel.
CCH-Naucalpan.
201-A
Matemáticas II.
miércoles, 10 de abril de 2013
Angulos Opuestos por el vértice.
Si el ángulo a y b son opuestos por el vértice.
Angulo a = 60 grados y el Angulo b = 3x-3
Obten el valor de X y del ángulo b.
Sabemos que si 2 ángulos son opuestos por el vértice sus medidas son iguales. Entonces:.
3x-3 = 60
3x = 60+3
3x = 63
x = 63/3
x = 21
Ya tenemos el valor de x ahora lo sustituimos en b = 3x-3 para saber el valor del ángulo b.
b = 3(21)-3
b = 63-3
b = 60
Y efectivamente el ángulo mide 60 grados como el ángulo a. FIN.
De Jesús Vargas Daniel.
CCH-Naucalpan.
201-A
Matemáticas II.
Angulo a = 60 grados y el Angulo b = 3x-3
Obten el valor de X y del ángulo b.
Sabemos que si 2 ángulos son opuestos por el vértice sus medidas son iguales. Entonces:.
3x-3 = 60
3x = 60+3
3x = 63
x = 63/3
x = 21
Ya tenemos el valor de x ahora lo sustituimos en b = 3x-3 para saber el valor del ángulo b.
b = 3(21)-3
b = 63-3
b = 60
Y efectivamente el ángulo mide 60 grados como el ángulo a. FIN.
De Jesús Vargas Daniel.
CCH-Naucalpan.
201-A
Matemáticas II.
sábado, 6 de abril de 2013
Ángulos Internos de un polígono.
Ejercicio 1.
Los ángulos internos de un polígono se obtienen dividiendo el polígono en triángulos, y como sabemos que los ángulos internos de un triángulo miden 180º, solo multiplicamos 180 por el número de triángulos en los que que dividimos el polígono y listo.
Pero hay una forma más Fácil usando la formula: Lados del poligono - 2 ( 180º ) .
Osea numero de lados del polígono menos 2 por 180.
Ejercicios.
A) Un polígono de 38 lados.
Solo sustituimos en la fórmula :Lados del polígono - 2 (180)
38 -2 (180) =
36 (180) = 6480º Es la suma de los ángulos internos del polígono.
B) Un polígono de 10 lados:
Hacemos lo mismo: 10 - 2 (180) =
8 (180) = 1440º Es la suma de los ángulos internos del polígono.
C) Un polígono de: 17 lados:
Hacemos lo mismo: 17-2 (180) =
15 (180) = 2700º Es la suma de los ángulos internos del polígono.
Los ángulos internos de un polígono se obtienen dividiendo el polígono en triángulos, y como sabemos que los ángulos internos de un triángulo miden 180º, solo multiplicamos 180 por el número de triángulos en los que que dividimos el polígono y listo.
Pero hay una forma más Fácil usando la formula: Lados del poligono - 2 ( 180º ) .
Osea numero de lados del polígono menos 2 por 180.
Ejercicios.
A) Un polígono de 38 lados.
Solo sustituimos en la fórmula :Lados del polígono - 2 (180)
38 -2 (180) =
36 (180) = 6480º Es la suma de los ángulos internos del polígono.
B) Un polígono de 10 lados:
Hacemos lo mismo: 10 - 2 (180) =
8 (180) = 1440º Es la suma de los ángulos internos del polígono.
C) Un polígono de: 17 lados:
Hacemos lo mismo: 17-2 (180) =
15 (180) = 2700º Es la suma de los ángulos internos del polígono.
miércoles, 3 de abril de 2013
Teoremas.
Ejercicio 1.
Determina cuales son las medidas de los ángulos X y Y. Y justifica tu respuesta basándote en algún teorema de ángulos.
Analizando la figura nos damos cuenta que el ángulo X es alterno interno al ángulo de 80º. Entonces ya sabemos que el ángulo X vale 80º grados.
Y para saber cuanto mide el ángulo Y es muy facil solo nos damos cuenta que entre el ángulo de 40º, el ángulo x=80 y Y, se forma un ángulo de 180º. Entonces lo que tenemos que hacer es una facil resta y unas sumas.
Decimos: 40º + 80º = 120º
Entonces entre los 2 ángulos que conocemos sus medidas formamos 120º, para 180º.
180º - 120º = 60º
Entonces ya sabemos que el ángulo Y mide 60º.
De Jesús Vargas Daniel.
CCH-Naucalpan.
201-A
Matemáticas II.
Determina cuales son las medidas de los ángulos X y Y. Y justifica tu respuesta basándote en algún teorema de ángulos.
Analizando la figura nos damos cuenta que el ángulo X es alterno interno al ángulo de 80º. Entonces ya sabemos que el ángulo X vale 80º grados.
Y para saber cuanto mide el ángulo Y es muy facil solo nos damos cuenta que entre el ángulo de 40º, el ángulo x=80 y Y, se forma un ángulo de 180º. Entonces lo que tenemos que hacer es una facil resta y unas sumas.
Decimos: 40º + 80º = 120º
Entonces entre los 2 ángulos que conocemos sus medidas formamos 120º, para 180º.
180º - 120º = 60º
Entonces ya sabemos que el ángulo Y mide 60º.
De Jesús Vargas Daniel.
CCH-Naucalpan.
201-A
Matemáticas II.
lunes, 25 de marzo de 2013
Semejanza de Triángulos.
Ejercicio 1.
Demuestra que el triángulo I es semejante al Triángulo II.
Paso 1: Reconocer el postulado en este caso sera LAL.
Paso 2: Vemos que lados de los triangulos son semejantes. (Lado chico con chico y grande con grande)
Paso 3: Los acomodamos como si los fueramos a dividir cada lado con su lado semejante así:
Para el segundo caso utilizamos la ley del sandwich ya que teniamos una fraccion y asi es más facil.
Paso 3: Resolvemos la ley de sandwich y nos queda 20/15.
Paso 4: Dividimos nuestros 2 resultados: 12/9 y 20/15. Y el resultado de nuestras 2 divisiones debe ser el mismo. En este caso 1.3 y así nos damos cuenta que los triangulos son semejantes.
Paso 5: Por último nos fijamos que los angulos de los 2 triángulos son iguales (90º).
FIN.
De Jesus Vargas Daniel.
CCH-Naucalpan.
201-A
Matemáticas II.
sábado, 16 de marzo de 2013
Congruencia de Triángulos.
Encuentra el valor de X y Y. Utilizando los postulados de congruencia: (LLL, LAL, ALA).
Lo primero que hay que hacer es reconocer el postulado de congruencia.
En este caso es ALA (angulo lado angulo), porque los 2 angulos de arriba son iguales,y los angulos rectos de abajo son iguales tambien, y el lado que se encuentra entre estos dos como es un lado compartido tambien es congruente.
Después, lo podemos resolver por medio de ecuaciones así:
decimos:
2x = 3y + 8
x = 2y
Como ya sabemos que x vale 2y.
solo lo sustituimosen la primera ecuación.
2(2y) = 3y+8
4y = 3y + 8
4y - 3y = 8
y = 8
Ya tenemos el valor de Y, falta el de X, para obtenerlo solo volvemos a sustituir en la misma ecuación.
2x = 3(8) + 8
2x = 24 + 8
2x = 32
x = 32/2
x = 16
Para comprobar solo sustituimos en los lados del triangulo con los valores de X (16) y de Y (8).
Así:
De Jesús Vargas Daniel.
CCH- Naucalpan.
201-A
Matemáticas II.
Lo primero que hay que hacer es reconocer el postulado de congruencia.
En este caso es ALA (angulo lado angulo), porque los 2 angulos de arriba son iguales,y los angulos rectos de abajo son iguales tambien, y el lado que se encuentra entre estos dos como es un lado compartido tambien es congruente.
Después, lo podemos resolver por medio de ecuaciones así:
decimos:
2x = 3y + 8
x = 2y
Como ya sabemos que x vale 2y.
solo lo sustituimosen la primera ecuación.
2(2y) = 3y+8
4y = 3y + 8
4y - 3y = 8
y = 8
Ya tenemos el valor de Y, falta el de X, para obtenerlo solo volvemos a sustituir en la misma ecuación.
2x = 3(8) + 8
2x = 24 + 8
2x = 32
x = 32/2
x = 16
Para comprobar solo sustituimos en los lados del triangulo con los valores de X (16) y de Y (8).
Así:
De Jesús Vargas Daniel.
CCH- Naucalpan.
201-A
Matemáticas II.
martes, 12 de marzo de 2013
Construcción de un Hexágono.
Construye un hexágono regular usando solo regla y compás.
1º Paso: Traza un circulo cualquiera, y traza a este su diámetro y obtén la mediatriz de su diámetro.
2º Paso: En donde se crucen las 2 lineas sera el punto O.
3º Paso: Después apoyándote en donde el diámetro corta al circulo traza 2 arcos del tamaño del radio.
4º Paso: en donde estos arcos corten al circulo pon puntos y al final solo unelos.
Imágenes:
Paso 1 y 2.
Paso 3 y 4.
De Jesús Vargas Daniel.
Grupo 201-A
CCH-Naucalpan.
Matemáticas II.
1º Paso: Traza un circulo cualquiera, y traza a este su diámetro y obtén la mediatriz de su diámetro.
2º Paso: En donde se crucen las 2 lineas sera el punto O.
3º Paso: Después apoyándote en donde el diámetro corta al circulo traza 2 arcos del tamaño del radio.
4º Paso: en donde estos arcos corten al circulo pon puntos y al final solo unelos.
Imágenes:
Paso 1 y 2.
Paso 3 y 4.
De Jesús Vargas Daniel.
Grupo 201-A
CCH-Naucalpan.
Matemáticas II.
miércoles, 6 de marzo de 2013
Centro de un Círculo.
Ejercicio 1.
Encuentra el el centro de un circulo.
Paso 1 Trazamos 2 cuerdas dentro del circulo mas o menos del mismo tamaño.
Paso 2 Sacamos la mediatriz de cada cuerda.
Paso 3 Trazamos las mediatrices y en donde se corten el es centro del circulo.
Encuentra el el centro de un circulo.
Paso 1 Trazamos 2 cuerdas dentro del circulo mas o menos del mismo tamaño.
Paso 2 Sacamos la mediatriz de cada cuerda.
Paso 3 Trazamos las mediatrices y en donde se corten el es centro del circulo.
De Jesús Vargas Daniel.
CCH-Naucalpan.
201-A.
Matemáticas II.
jueves, 28 de febrero de 2013
Desigualdad de Triángulos.
En todo triangulo la suma de las medidas de dos de sus lados deben ser mayores a la medida del lado restante.
Ejercicio 1.
Lado 1: 4
Lado 2: 5
Lado 3: 7
Lo que tenemos que hacer es primero sumar 4+5 después 4+7 y al último 5+7
4+5 = 9 > 7
Cuatro más cinco es la suma de dos lados, el resultado es 9, y es mayor a 7 que es el otro lado restante.
4+7 = 11 > 5
Cuatro más siete es la suma de dos lados, el resultado es 11, y es mayor que 5 el otro lado restante.
5+7 = 12 > 4
Cinco más siete es la suma de dos lados, 12 es el resultado y es mayor que 4 el lado restante.
Ya hecho esto construimos el triángulo.
Ejercicio 1.
Lado 1: 4
Lado 2: 5
Lado 3: 7
Lo que tenemos que hacer es primero sumar 4+5 después 4+7 y al último 5+7
4+5 = 9 > 7
Cuatro más cinco es la suma de dos lados, el resultado es 9, y es mayor a 7 que es el otro lado restante.
4+7 = 11 > 5
Cuatro más siete es la suma de dos lados, el resultado es 11, y es mayor que 5 el otro lado restante.
5+7 = 12 > 4
Cinco más siete es la suma de dos lados, 12 es el resultado y es mayor que 4 el lado restante.
Ya hecho esto construimos el triángulo.
De Jesús Vargas Daniel.
CCH-Naucalpan.
201-A.
Matemáticas II.
sábado, 23 de febrero de 2013
Rectas y puntos importantes del triángulo.
Bisectrices: Son las rectas que dividen a cada ángulo del triángulo en 2 ángulos iguales. Y el punto en donde se cruzan las 3 Bisectrices en el incentro.
Para realizar esto se hace lo siguiente:
1) Se tiene que sacar la bisectriz de cada ángulo del triángulo, estas se obtienen trazando con el compás apoyado en el vértice, un arco que corte los 2 lados de un ángulo del triángulo, en donde el arco corte los dos lados del ángulo pondremos un punto.
2) En estos puntos nos apoyaremos con el compás de nuevo para trazar un pequeño arco hacia arriba, primero apoyándose en uno de los puntos y luego en otro, ésto se hace con la misma abertura del compás.
Para realizar esto se hace lo siguiente:
1) Se tiene que sacar la bisectriz de cada ángulo del triángulo, estas se obtienen trazando con el compás apoyado en el vértice, un arco que corte los 2 lados de un ángulo del triángulo, en donde el arco corte los dos lados del ángulo pondremos un punto.
2) En estos puntos nos apoyaremos con el compás de nuevo para trazar un pequeño arco hacia arriba, primero apoyándose en uno de los puntos y luego en otro, ésto se hace con la misma abertura del compás.
3) Después solo unimos el punto en donde se cruzaron los 2 últimos arcos con el vértcice y lísto.
Repetimos el mismo procedimiento hasta tener las bisectrices de los 3 águlos.
Después en donde se cortan las tres bisectrices (si es necesario alargarlas lo puedes hacer para que veas en donde se cortan) apoyamos en compás el el incentro (que es en donde se cortan las 3 bisectrices)
y lo abrimos hacia uno de los lados del triángulo y trazamos un círculo que debe quedar dentro del triángulo.
NOTA: En un triángulo equilátero el incentro baricentro y gravicentro quedan en el mismo punto.
De Jesús Vargas Daniel.
CCH-Naucalpan.
201-A
Matemáticas II.
martes, 19 de febrero de 2013
Triangulos.
Ejercicio número 1.
Si un triangulo tiene los siguientes ángulos:
a) 40º, 25º, 115º es un triángulo: Obtusángulo porque tiene un ángulo mayor de 90º y dos menores de 90º.
Sería algo más o menos así.
b) 42º, 48º, 90º es un triangulo: Rectángulo porque tiene un ángulo de 90º exactos.
Este sería algo así.
c) 60º, 60º, 60º, es un triángulo: Equiángulo porque todos sus ángulos miden 90º.
Este sería así:
d) 80º, 45º, 55º es un triángulo: Actuángulo porque todos sus ángulos son menores de 90º.
Este sería mas o menos así:
Si un triangulo tiene los siguientes ángulos:
a) 40º, 25º, 115º es un triángulo: Obtusángulo porque tiene un ángulo mayor de 90º y dos menores de 90º.
Sería algo más o menos así.
b) 42º, 48º, 90º es un triangulo: Rectángulo porque tiene un ángulo de 90º exactos.
Este sería algo así.
c) 60º, 60º, 60º, es un triángulo: Equiángulo porque todos sus ángulos miden 90º.
Este sería así:
d) 80º, 45º, 55º es un triángulo: Actuángulo porque todos sus ángulos son menores de 90º.
Este sería mas o menos así:
De Jesús Vargas Daniel
CCH-N.
201-A.
Matemáticas II.
sábado, 16 de febrero de 2013
Clasificación de triángulos.
Podemos clasificar los Triángulos de 2 formas por sus lados y por sus ángulos.
Por sus Lados se pueden clasificar como:
Isósceles: tiene dos lados iguales y uno diferente.
Equilátero: tiene sus tres lados iguales.
Escaleno: tiene sus tres lados diferentes.
Por sus ángulos se pueden clasificar como:
Triangulo rectángulo: tiene un ángulo de 90º enfrente de la hipotenusa.
Acutángulo: sus tres ángulos son menores de 90º.
Obtusángulo: tiene un ángulo mayor a 90º pero menor de 180º.
Bibliografía:
http://queenlnf.blogspot.mx/2009/04/clasificacion-de-triangulos-segun-sus.html
http://www.amschool.edu.sv/paes/g1.htm
http://ar.answers.yahoo.com/question/index?qid=20100807105837AASBW8o
De Jesús Vargas Daniel.
201-A.
CCH-N.
Matemáticas II.
Por sus Lados se pueden clasificar como:
Isósceles: tiene dos lados iguales y uno diferente.
Equilátero: tiene sus tres lados iguales.
Escaleno: tiene sus tres lados diferentes.
Por sus ángulos se pueden clasificar como:
Triangulo rectángulo: tiene un ángulo de 90º enfrente de la hipotenusa.
Acutángulo: sus tres ángulos son menores de 90º.
Obtusángulo: tiene un ángulo mayor a 90º pero menor de 180º.
Bibliografía:
http://queenlnf.blogspot.mx/2009/04/clasificacion-de-triangulos-segun-sus.html
http://www.amschool.edu.sv/paes/g1.htm
http://ar.answers.yahoo.com/question/index?qid=20100807105837AASBW8o
De Jesús Vargas Daniel.
201-A.
CCH-N.
Matemáticas II.
Ejercicios de Ángulos.
A partir de la siguiente figura menciona:
a) Un par de ángulos opuestos por el vértice.
R= < FDE y < FBA.
b) El suplemento del ángulo formado por los rayos DFE.
R= < DFE + < FBA = 180º .
c) Un segmento que sea perpendicular al segmento FC si el ángulo formado por los rayos CFD = 90º.
R= CFA.
d) Menciona un par de ángulos adyacentes que no sean suplementarios.
R= < FDE con < FCD
e) ¿Es cierto que FC biseca a AD?
R= Sí porque pasa a la mitad del segmento.
De Jesús Vargas Daniel.
CCH-N.
201-A.
Matemáticas II.
a) Un par de ángulos opuestos por el vértice.
R= < FDE y < FBA.
b) El suplemento del ángulo formado por los rayos DFE.
R= < DFE + < FBA = 180º .
c) Un segmento que sea perpendicular al segmento FC si el ángulo formado por los rayos CFD = 90º.
R= CFA.
d) Menciona un par de ángulos adyacentes que no sean suplementarios.
R= < FDE con < FCD
e) ¿Es cierto que FC biseca a AD?
R= Sí porque pasa a la mitad del segmento.
De Jesús Vargas Daniel.
CCH-N.
201-A.
Matemáticas II.
miércoles, 13 de febrero de 2013
Ángulos.
Ángulo adyacente: Los ángulos adyacentes son aquellos que comparten el vértice y alguno de sus lados.
Ángulos opuestos por le vértice: Son en los que los lados de uno son semirrectas opuestas a los lados del otro.
Ángulos suplementarios: Son 2 ángulos que juntos suman 180º.
Ángulos complementarios: Son 2 ángulos que juntos suman 90º.
Ángulos llanos: Son los que miden 180º exactamente.
Ángulos rectos: Son los que miden 90º exactamente.
Ángulos agudos: Son los que miden menos de 90º.
Ángulos obtusos: Son los que miden más de 90º pero menos de 180º.
Bibliografía:
http://www.disfrutalasmatematicas.com/geometria/angulos-adyacentes.html
http://www.disfrutalasmatematicas.com/geometria/angulos-opuestos-vertice.html
http://eca-geometriabasica.blogspot.mx/2009/07/angulos-complementarios-y.html
http://www.taringa.net/posts/ciencia-educacion/12586306/Definicion-de-un-angulo-llano.html
http://www.esacademic.com/dic.nsf/es_mediclopedia/55163/%C3%A1ngulo
De Jesús Vargas Daniel.
CCH-Naucalpan.
Grupo 201-A.
Matemáticas II.
Ángulos opuestos por le vértice: Son en los que los lados de uno son semirrectas opuestas a los lados del otro.
Ángulos suplementarios: Son 2 ángulos que juntos suman 180º.
Ángulos complementarios: Son 2 ángulos que juntos suman 90º.
Ángulos llanos: Son los que miden 180º exactamente.
Ángulos rectos: Son los que miden 90º exactamente.
Ángulos agudos: Son los que miden menos de 90º.
Ángulos obtusos: Son los que miden más de 90º pero menos de 180º.
Bibliografía:
http://www.disfrutalasmatematicas.com/geometria/angulos-adyacentes.html
http://www.disfrutalasmatematicas.com/geometria/angulos-opuestos-vertice.html
http://eca-geometriabasica.blogspot.mx/2009/07/angulos-complementarios-y.html
http://www.taringa.net/posts/ciencia-educacion/12586306/Definicion-de-un-angulo-llano.html
http://www.esacademic.com/dic.nsf/es_mediclopedia/55163/%C3%A1ngulo
De Jesús Vargas Daniel.
CCH-Naucalpan.
Grupo 201-A.
Matemáticas II.
martes, 12 de febrero de 2013
Construcciones Geométricas Básicas.
Ejercicio 1.
2A -1B.
1)Paso 1 Lo primero sera poner un punto ''P''.
2)Después con el compás. Mediremos nuestro segmento AB Osea el A). Y apoyándonos en el punto ''P'' trazaremos un medio circulo y después haremos lo mismo pero esta vez apoyándonos en cualquier parte del medio circulo trazado anteriormente.
3)Ya habiendo trazado el otro circulo podemos poner un punto cualquiera ''Q'' que se encuentre en el círculo y unirlo con el punto ''P'' y ya tenemos nuestra recta 2A. Solo falta restarle 1B osea el segmento CD.
4)Para lo que mediremos con nuestro compás el segmento CD y apoyando en el punto ''Q'' trazamos un medio circulo y en el punto que toque con la linea sera el nuevo punto ''Q'' ya que lo que hicimos fue restarle 1B y listo.
2A -1B.
1)Paso 1 Lo primero sera poner un punto ''P''.
2)Después con el compás. Mediremos nuestro segmento AB Osea el A). Y apoyándonos en el punto ''P'' trazaremos un medio circulo y después haremos lo mismo pero esta vez apoyándonos en cualquier parte del medio circulo trazado anteriormente.
3)Ya habiendo trazado el otro circulo podemos poner un punto cualquiera ''Q'' que se encuentre en el círculo y unirlo con el punto ''P'' y ya tenemos nuestra recta 2A. Solo falta restarle 1B osea el segmento CD.
4)Para lo que mediremos con nuestro compás el segmento CD y apoyando en el punto ''Q'' trazamos un medio circulo y en el punto que toque con la linea sera el nuevo punto ''Q'' ya que lo que hicimos fue restarle 1B y listo.
lunes, 11 de febrero de 2013
Elementos geométricos.
domingo, 3 de febrero de 2013
Función Estándar a General.
Conociendo el Vértice y El valor de ''a'' podemos encontrar la forma general tansolo sustituyendo en la forma estándar: a(x-h)^2+k.
Ejercicio 1:
A = 4
Vértice = (1,3)
Paso uno reconocer a h y k las dos ultimas los obtendremos observando los puntos del vértice 1 y 3.
a = 4
h = 1
k = 3
Paso 2 sustituir en la formula a(x-h)^2+k.
Ejercicio 1:
A = 4
Vértice = (1,3)
Paso uno reconocer a h y k las dos ultimas los obtendremos observando los puntos del vértice 1 y 3.
a = 4
h = 1
k = 3
Paso 2 sustituir en la formula a(x-h)^2+k.
De Jesús Vargas Daniel.
201-A
CCH-Naucalpan.
jueves, 31 de enero de 2013
Conversión de Forma General a Forma Estándar.
Caso 2: Cuando el coeficiente de cuadrático es mayor a ''1''.
Ejercicio 1:
4x^2 - 8x + 7
Elementos de la gráfica.
Ramas: Arriba
Concavidad: Positiva.
Eje: 1
Mínima: 3
Vértice: (1,3)
De Jesús Vargas Daniel.
CCH-Naucalpan.
201- A
Ejercicio 1:
4x^2 - 8x + 7
Elementos de la gráfica.
Ramas: Arriba
Concavidad: Positiva.
Eje: 1
Mínima: 3
Vértice: (1,3)
De Jesús Vargas Daniel.
CCH-Naucalpan.
201- A
martes, 29 de enero de 2013
Conversión de Forma general a forma Estándar.
Ejercicio 1.
y = x^2 +6x + 7
Paso 1 reconer a b y c .
a: 1
b: 6
c: 7
Paso 2 aplicar la fórmula ( b/2 ) ^2.
Paso 3 sumar y restar el resultado anterior en la ecuación principal.
y = x^2 +6x +9 -9 +7
Los primero 3 terminos corresponden a un tcp que tenemos que factorizar para obtener un binomio al cuadrado.
Paso 4 reconocer
a : 1
h : -3
k : -2
Después tabulamos.
Tenemos que el vértice es -3,-2 pero necesitamos más puntos para tabular y graficar, así que tomaremos dos valores para x que sean mayores de -3 y dos menores de -3.
Nos quedará así ya tabulado y graficado.

Elementos de la parábola.
Ramas: Arriba.
Concavidad: Positiva.
Eje: -3
Mínima: -2
Vértice -3,-2.
De Jesús Vargas Daniel.
CCH-Naucalpan.
201-A
Matemáticas 2.
y = x^2 +6x + 7
Paso 1 reconer a b y c .
a: 1
b: 6
c: 7
Paso 2 aplicar la fórmula ( b/2 ) ^2.
Paso 3 sumar y restar el resultado anterior en la ecuación principal.
y = x^2 +6x +9 -9 +7
Los primero 3 terminos corresponden a un tcp que tenemos que factorizar para obtener un binomio al cuadrado.
Paso 4 reconocer
a : 1
h : -3
k : -2
Después tabulamos.
Tenemos que el vértice es -3,-2 pero necesitamos más puntos para tabular y graficar, así que tomaremos dos valores para x que sean mayores de -3 y dos menores de -3.
Nos quedará así ya tabulado y graficado.

Elementos de la parábola.
Ramas: Arriba.
Concavidad: Positiva.
Eje: -3
Mínima: -2
Vértice -3,-2.
De Jesús Vargas Daniel.
CCH-Naucalpan.
201-A
Matemáticas 2.
domingo, 27 de enero de 2013
Comparación de Gráficas.
Forma estándar.
y = a ( x - h )^2 + k.
En donde a h y k según sus valores la gráfica se moverá de derecha a izquierda de arriba hacia abajo o se ensanchará o adelgazara.
Ejercicio: Comparar las gráficas 1 y 2 y escribir porque quedan de diferente forma.
1) y = x^2
Paso 1
Tabular con los valores del -3 al 3.
Reconocemos a h y k de la ecuación y = x^2.
a = 1
h = 0
k = 0
Paso 2 Graficar.
2) y = 3x^2
Así queda graficado y tabulado.
a = 3
h = 0
k = 0
Ahora la primera grafica queda muy corta y con el vértice en 0,0 porque ''a'' vale 1.
Y en la segunda grafica queda con vértice en 0,0 pero más larga porque ''a'' vale 3.
De Jesús Vargas Daniel.
CC-H Naucalpan.
201-A.
jueves, 24 de enero de 2013
Análisis del discriminante.
Graficar la función : f(x) = -x^2 + 3x
Paso 1 reconocer a b y c.
a: -1
b: +3
c: 0
Paso 2 usar la formula general para obtener 2 puntos en x y en y.
Nos quedarán 2 puntos para x que son 0 y 3. Y para y serán 0 y 0 igual que siempre.

Lo que sigue es obtener el Vértice. Para eso utilizaremos la formula de x = -b/2(a).
Nos queda así.

Después sustituimos el valor de x en f(x) osea ''y'' para obtener el punto ''y'' y completar la coordenada del vértice. Y nos queda así.

Entonces sabemos que el vértice queda en el punto 3/2 , 18/8.
Entonces todos los puntos quedaran así.
x y
0 0
3/2 18/8
3 0
Y ahora solo graficamos. Y nos queda así.

De Jesús Vargas Daniel.
CHH-Naucalpan.
Grupo 201-A
Matemáticas II.
Paso 1 reconocer a b y c.
a: -1
b: +3
c: 0
Paso 2 usar la formula general para obtener 2 puntos en x y en y.
Nos quedarán 2 puntos para x que son 0 y 3. Y para y serán 0 y 0 igual que siempre.

Lo que sigue es obtener el Vértice. Para eso utilizaremos la formula de x = -b/2(a).
Nos queda así.

Después sustituimos el valor de x en f(x) osea ''y'' para obtener el punto ''y'' y completar la coordenada del vértice. Y nos queda así.

Entonces sabemos que el vértice queda en el punto 3/2 , 18/8.
Entonces todos los puntos quedaran así.
x y
0 0
3/2 18/8
3 0
Y ahora solo graficamos. Y nos queda así.

De Jesús Vargas Daniel.
CHH-Naucalpan.
Grupo 201-A
Matemáticas II.
Suscribirse a:
Comentarios (Atom)