Como convertir grados a Radianes.

Grados a Radianes.

Con esta simple fórmula podemos convertir Grados en Radianes.

Radianes a Grados.

Con esta simple fórmula podemos convertir Radianes en Grados.

Como Convertir los decimales a Minutos y Segundos.

Ejemplo.
45.891°
1ro tomamos los decimales .891 lo multiplicamos por 60 y nos da de resultado 53.46.
2do tomamos los nuevos decimales que obtuvimos .46 los multiplicamos por 60 y nos da como resultado 27.6 que se redondea a 28.
3ro Resultado final: 45° 53' y 28'' Osea 45 grados, 53 minutos y 28 segundos.

Fuente: http://www.ehowenespanol.com/conversion-grados-radianes-como_113664/

De Jesús Vargas Daniel.
CCH-Naucalpan.
201-A
Matemáticas II.

Ley del Seno y Coseno.

Ley del Seno:

Nos demuestra que los lados de un triángulo son  proporcionales a los senos de los ángulos opuestos.

Ley del Coseno:

Nos demuestra que el cuadrado de un lado es igual a la suma de los cuadrados de los otros lados menos el doble del producto de estos lados por el coseno del ángulo comprendido.

a² = b² + c² - 2 bc * Cos (A)

b² = a² + c² - 2 ac * Cos (B)

c² = a² + b² - 2 ab * Cos (C)


Fuente: http://docente.ucol.mx/narahita/leyes/sen2.htm

De Jesús Vargas Daniel.
CCH-Naucalpan.
201-A
Matemáticas II.

Ecuaciones con Razones Trigonométricas.

Ejercicio 1.
Obtener el resultado de la siguiente función.
6 (SEN 30°) (COS 30°) + 8(TAN 30°) (COS 45°) =

Paso 1°: Obtener lo que esta dentro de paréntesis, osea lo senos y cosenos.
6 (0.5) (0.86) + 8 ( 0.57)  (0.70) =
Paso 2°: Hacer las multiplicaciones correspondientes.
3 * 0.86 + 4.56 * 0.70 =
2.58 + 3.19 = 5.77

El resultado de esta función es 5.77.

De Jesús Vargas Daniel.
CCH-Naucalpan.
201-A
Matemáticas II.

Funciones Trigonométricas II.

Problema 1.
Un teleférico recorre 8 metros y se  eleva a una la altura de 1.5 metros ¿Cual sera el ángulo de elevación de la subida, y la distancia entre las 2 montañas entre las que se encuentra el teleférico?

Para saber el ángulo, usamos la función trigonométrica de Seno, ya que tenemos las medidas de cateto opuesto y la hipotenusa.
Nota: A = a ángulo.

Sen A = 1.5/8
Sen A = 0.18
A= Sen-¹ (0.18)
A= 10.36

Ya obtuvimos el ángulo ahora falta la distancia entre las montañas (x). Para obtener esto solo utilizamos teorema de pitagoras.

c² = a² + b²
8² = 1.5² + b²
64 = 2.25 + b²
64-2.25 = b²
61.75 = b²
7.85 = b

Y ya obtuvimos el lado restante del triángulo que es la distancia entre las 2 montañas.

De Jesús Vargas Daniel.
CCH-Naucalpan.
201-A
Matemáticas II.

Funciones Trigonométricas.

Ejercicio 1.
Obtener las funciones trigonométricas y ángulos del siguiente triángulo.

Las funciones trigonométricas son 6 :
Seno, Coseno y Tangente. Seno se obtiene dividiendo Cateto opuesto/ Hipotenusa.
                                         Coseno se obtiene dividiendo Cateto adyacente/ Hipotenusa.
                                         Tangente se obtiene dividiendo Cateto opuesto / Cateto adyacente.
Y sus Inversas: Cosecante: Hipotenusa / Cateto Opuesto.
                        Secante: Hipotenusa / Cateto adyacente.
                        Cotangente: Cateto adyacente / Cateto opuesto.
(Los catetos se pueden identificar porque son los 2 lados con los que se forma el angulo de 90°)
Paso 1 : Obtener las funciones Trigonométricas.

Paso 2 : Obtener las Medidas de los Ángulos.

Para obtener la medida del ángulo que nos piden podemos despejar a seno así:

Nota A = angulo.

Sen A = 0.83

A= Sen-¹ (0.83)    

A= 56.09°

Y esa es la medida del ángulo que nos piden.

De Jesús Vargas Daniel.

CCH-Naucalpan.

201-A

Maremáticas II.

    

Volumenes.

Ejercicio 1.

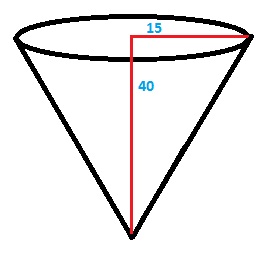
Calcula el volumen de un cono si el radio de su base mide 15 cm y la altura 40.

Solo debemos aplicar la formula para saber el volumen del cono : ¶ . r² . h / 3

Osea 'Pi' por radio al cuadrado por altura entre 3. 

Paso 1: Solo sustituir en la formula y resolver loas operaciones.

¶ * 225 * 40 / 3

Resultado: 9424.77 cm ³

Y ese es el volumen del cono.

De Jesús Vargas Daniel.

CCH-Naucalpan.

201-A

Matemáticas II.

Areas.

Ejercicio 1.

Un espejo circular mide 1.25 metros de diámetro ¿Que área tiene?

Solo hay que saber que la formula para sacar el área de un circulo es 3.1416 x r^2. Osea pi por radio al cuadrado.

En este caso nos dan el diámetro, pero nosotros necesitamos el radio entonces dividimos el diámetro entre 2. Obtenemos .625.

Ahora ya aplicamos la formula, primero hacemos .625 al cuadrado, eso nos da de resultado .3906, y ya esto lo multiplicamos por pi, esto nos da de resultado 1.2271 y eso es el área del espejo.

De Jesús Vargas Daniel.
CCH-Naucalpan.
201-A
Matemáticas II.