Funciones Trigonométricas.

Ejercicio 1.
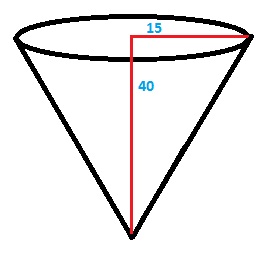
Obtener las funciones trigonométricas y ángulos del siguiente triángulo.

Las funciones trigonométricas son 6 :
Seno, Coseno y Tangente. Seno se obtiene dividiendo Cateto opuesto/ Hipotenusa.
                                         Coseno se obtiene dividiendo Cateto adyacente/ Hipotenusa.
                                         Tangente se obtiene dividiendo Cateto opuesto / Cateto adyacente.
Y sus Inversas: Cosecante: Hipotenusa / Cateto Opuesto.
                        Secante: Hipotenusa / Cateto adyacente.
                        Cotangente: Cateto adyacente / Cateto opuesto.
(Los catetos se pueden identificar porque son los 2 lados con los que se forma el angulo de 90°)
Paso 1 : Obtener las funciones Trigonométricas.

Paso 2 : Obtener las Medidas de los Ángulos.

Para obtener la medida del ángulo que nos piden podemos despejar a seno así:

Nota A = angulo.

Sen A = 0.83

A= Sen-¹ (0.83)    

A= 56.09°

Y esa es la medida del ángulo que nos piden.

De Jesús Vargas Daniel.

CCH-Naucalpan.

201-A

Maremáticas II.

    

Volumenes.

Ejercicio 1.

Calcula el volumen de un cono si el radio de su base mide 15 cm y la altura 40.

Solo debemos aplicar la formula para saber el volumen del cono : ¶ . r² . h / 3

Osea 'Pi' por radio al cuadrado por altura entre 3. 

Paso 1: Solo sustituir en la formula y resolver loas operaciones.

¶ * 225 * 40 / 3

Resultado: 9424.77 cm ³

Y ese es el volumen del cono.

De Jesús Vargas Daniel.

CCH-Naucalpan.

201-A

Matemáticas II.

Areas.

Ejercicio 1.

Un espejo circular mide 1.25 metros de diámetro ¿Que área tiene?

Solo hay que saber que la formula para sacar el área de un circulo es 3.1416 x r^2. Osea pi por radio al cuadrado.

En este caso nos dan el diámetro, pero nosotros necesitamos el radio entonces dividimos el diámetro entre 2. Obtenemos .625.

Ahora ya aplicamos la formula, primero hacemos .625 al cuadrado, eso nos da de resultado .3906, y ya esto lo multiplicamos por pi, esto nos da de resultado 1.2271 y eso es el área del espejo.

De Jesús Vargas Daniel.
CCH-Naucalpan.
201-A
Matemáticas II.

Áreas.

Ejercicio 1.

¿Cual es el perímetro de un terreno pentagonal si  cada lado mide 13 metros?

Esto es muy fácil sabemos que un pentágono tiene 5 lados, y que cada lado mide 13 metros, entonces lo único que hay que hacer es multiplicar 5 x 13 = 65 m.

De Jesús Vargas Daniel.
CCH-Naucalpan.
201-A
Matemáticas II.

Angulos Opuestos por el vértice.

Si el ángulo a y b son opuestos por el vértice.
Angulo a = 60 grados y el Angulo b = 3x-3

Obten el valor de X y del ángulo b.

Sabemos que si 2 ángulos son opuestos por el vértice sus medidas son iguales. Entonces:.
3x-3 = 60
3x = 60+3
3x = 63
x = 63/3
x = 21

Ya tenemos el valor de x ahora lo sustituimos en b = 3x-3 para saber el valor del ángulo b.
b = 3(21)-3
b = 63-3
b = 60

Y efectivamente el ángulo mide 60 grados como el ángulo a. FIN.

De Jesús Vargas Daniel.
CCH-Naucalpan.
201-A
Matemáticas II.

Ángulos Internos de un polígono.

Ejercicio 1.
Los ángulos internos de un polígono se obtienen dividiendo el polígono en triángulos, y como sabemos que los ángulos internos de un triángulo miden 180º, solo multiplicamos 180 por el número de triángulos en los que que dividimos el polígono y listo.
Pero hay una forma más Fácil usando la formula:  Lados del poligono - 2 ( 180º ) .
Osea numero de lados del polígono menos 2 por 180.
Ejercicios.
A) Un polígono de 38 lados.
Solo sustituimos en la fórmula :Lados del polígono - 2 (180)
                                               38 -2 (180) =
                                               36 (180) = 6480º Es la suma de los ángulos internos del polígono.

B) Un polígono de 10 lados:
Hacemos lo mismo: 10 - 2 (180) =
                               8 (180) = 1440º Es la suma de los ángulos internos del polígono.

C) Un polígono de: 17 lados:
Hacemos lo mismo: 17-2 (180) =
                               15 (180) = 2700º Es la suma de los ángulos internos del polígono.

Teoremas.

Ejercicio 1.

Determina cuales son las medidas de los ángulos X y Y. Y justifica tu respuesta basándote en algún teorema de ángulos.

Analizando la figura nos damos cuenta que el ángulo X es alterno interno al ángulo de 80º. Entonces ya sabemos que el ángulo X vale 80º grados.
Y para saber cuanto mide el ángulo Y es muy facil solo nos damos cuenta que entre el ángulo de 40º, el ángulo x=80 y Y, se forma un ángulo de 180º. Entonces lo que tenemos que hacer es una facil resta y unas sumas.
Decimos: 40º + 80º = 120º
Entonces entre los 2 ángulos que conocemos sus medidas formamos 120º, para 180º.
180º - 120º = 60º
Entonces ya sabemos que el ángulo Y mide 60º. 


De Jesús Vargas Daniel.
CCH-Naucalpan.
201-A
Matemáticas II.